Probability
Probability means the chance or occurrence of an event.
P (Occurrence of an event) = 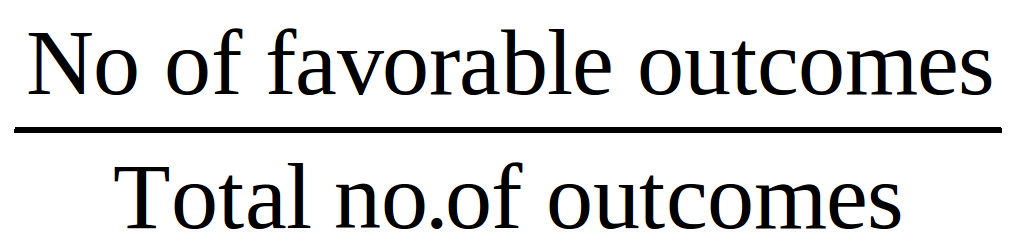
For an event A is sure to occur, P(A) = I
For an event A is sure not to occur, P(A) = 0
For any event, 0 < P (A) < I
Sample Space: It is defined in the context of a random experiment and denotes the set representing ail the possible outcomes of the random experiment, [e.g. Sample space when a coin is tossed is (Head, Tail). Sample space when a dice is thrown is (1, 2, 3,4,5, 6).
Mutually Exclusive Events: A set of events is mutually exclusive when the occurrence of any one of them means that the other events cannot occur. (If head appears on a coin, tail will not appear and vice versa.)
Equally Likely Events: If two events have the same probability, or chance of occurrence they are called equally likely events. (In a throw of a dice, the chance of I showing on the dice is equal to 2 is equal to 3 is equal to 4 is equal to 5 is equal to 6 appearing on the dice.)
Exhaustive Set of Events : A set of events that includes all the possibilities of the sample space is said to be an exhaustive set of events, (e.g. in a throw of a dice the number is less than three or more than or equal to three.)
Independent Events: An event is described as such if the occurrence of an event has no effect on the probability of the occurrence of another event, (If the first child of a couple is a boy, there is no effect on the chances of the second child being a boy.)
Expectation: The expectation of an individual is defined as
Probability of winning × Reward of winning.
1. Additional Law of Probability:
For two events A and B
P (A or B) = P (A) + P (B) – P (A and B)
If the events are mutually exclusive
P(A and B) = 0
2. Multiplication Law of Probability:
If the events A and B are independent
P(A and B) = P(A) × P(B)
3. Complement of an event:
P(A°) = I – P (A)
Example 1 Find the probability that a leap year chosen at random will have 53 Sundays.
Solution: A leap year has 366 days = 52 weeks + 2 days
2 days can be (Sun-Sat, Sun-Mon, Mon-Tue, Tue-Wed, Wed-Thurs, Thurs-Fri, Fri-Sat)
P (53 Sundays) = 
Example 2 3 coins are tossed together. Find the probability of getting
i) Exactly one head
ii) At least one head
iii) At most I head
Solution: Total number of cases when three coins are tossed together = 23 = 8. Now we will solve each of the above question one by one.
i) The cases of exactly one head are {(HTT)(TTH)(THT)}
ii) Probability of getting atleast one head = I - probability of getting no head = 1 - (1/8) = 7/8
iii) The cases of at most one head {(TTT)(HTT)(TTH)(THT)}
Example 3: Three unbiased coins are tossed. What is the probability of getting at least 2 heads?
Solution: P (at least 2 heads) = P (2 heads) + P (3 heads)
2 heads = {(H, H, T), (H, T, H), (T, H H)}
3 heads = {(H, H, T)}
P (at least 2 heads) = 
Example 4: An urn contains 9 red, 7 white and 4 black balls. If two balls are drawn at random. Find the probability that both the balls are red?
Solution:Total no of balls = 9-1-7 + 4 = 20
no. of ways of selecting 2 balls = 20C2
no. of ways of selecting 2 balls from 9 red balls = 9C2
P (Both red) = 
Example 5: The letters of the word LUCKNOW are arranged among themselves. Find the Probability of always having NOW in such words.
Solution: Required Probability =  =
= 
Other Quants Notes:







